This is a strategy which is based on calculating the size of each successive bet to ensure that the bankroll is spent rationally. The bettor himself calculates the probability of the event on which he wants to bet, and determines the appropriate betting amount. The player is supposed to protect the bankroll from losing.
When is Kelly’s criterion appropriate?
This strategy is optimal for experienced bettors. A player should already be able to calculate the probability of a certain event.
Kelly’s strategy is similar to a competition between the bank and the bank, as the one who has calculated the probability correctly wins. This strategy is considered an improved version of Value Betting. It is used when the odds are too high and the betting company has underestimated the probability of the event. Users of BK call such an event value.
The disadvantage of the Kelly criterion is that the player can misjudge the event. If he underestimates it, his winnings will be smaller, if he overestimates it, the bettor will lose completely.

How to use the strategy
This strategy will help to calculate a suitable bet on an event if the bettor has correctly estimated its probability, and, on the contrary, if the bettor has underestimated it.
The formula for calculating the probability is simple – 100% / odds.
Example: In a match between Barcelona and Real Madrid at odds of 1.40, the bettor assumes that the first opponent has a 71% probability of winning, while the bettor assumes that the second opponent will win with a 61% probability. Such a quotation is not overstated, as the bettor believes the odds from the office are less likely. Such a bet for using the strategy in question is better not to take.
To calculate a suitable bet for this strategy, use the following formula:
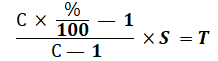
- where C – betting odds;
- % – percentage of probability of the event according to the bettor’s calculations;
- S – amount of the playing pot;
- T – amount of stake.
It is recommended to use the considered strategy only to experienced players, who successfully determine the probability of many events without lines and odds.
